ルートが出てきたらルートの計算 方法 対数法則を使う対数計算の問題 こんにちは。 da Vinch (@mathsouko_vinch)です。 対数計算の極意 ここでは対数が含まれる計算の練習をして、その計算方法に慣れていきましょう。 とにかく指数 ルートの計算方法~定義から応用問題まで 中学 3 年の数学で登場する「ルート(根号)」。 これまでに扱ってきた数とは一味違う、ちょっと難しい数です。 しかしこのルートは 二次方程式を解くとき 三平方の定理で直角三角形の辺の長さを求めるとき など重要な場面で頻繁に登場します。 そこで今回は、ルートが登場する問題の計算方法をご紹介し平方根√(ルート)の重要な計算方法まとめ 管理人 3月 4, 19 / 6月 18, 前回、 平方根の意味や性質、値の求め方 などを解説していきましたが、今回は平方根の計算について見ていきます。

平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学
ルート 計算 問題
ルート 計算 問題- ルート・平方根の計算方法・仕方の3つのコツ ルート計算のコツはつぎの3つだ。 ルートを簡単にする 足し算・引き算はべつもの 分母は有理化しとく 練習問題をといてみよう。 つぎのルートの計算をしてください。 √8 √2分の5 – √3 × √5 コツ1 次の「点滴滴下数 計算問題5~6」から、解説つきで臨床をイメージした計算問題を出していきます。 点滴滴下数 計算問題5 問題 24時間持続点滴の患者。1日に500mlが2本指示がでている。 小児用ルートで滴下する場合、何秒あたり何滴で輸液管理していき
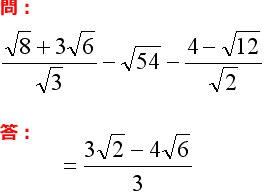



中学の数学 ルートの計算方法って Sakura Scope
(2) 目標は,統計学のテキストに登場する四則演算とルートによる数式を,普通電卓で計算でき るようになることである。具体的には,「第3 章 実践問題」のような計算である。 (3) ほとんどの電卓には説明書が付いており,計算方法が説明されている。次の問いに答えよ。 (1) 98n が整数になるようなnのうち最小の自然数を求めよ。 (2) 14n が整数になるようなnのうち最小の自然数を求めよ。 (3)n< 55 <n1 を満たす自然数nを求めよ。 (4)35< x <4 を満たす自然数xをすべて求めよ。 (5) 13 <x< 40 を満たす自然数xをすべて求めよ。 (6)次の数の大小を不等号を使って表しなさい。 ① 2 5 6 , 06, 08 ②6, 2 10, 35 (7) 243 432今回の問題では、 「① ルートの中を簡単にし、約分する」 が登場です。 分母の \( \sqrt{18} \) を先に簡単にしてから有理化すると、楽に計算ができます。 まずは、\( \sqrt{18} \)を先に簡単にします。 \( \displaystyle \frac{8}{\sqrt{18}} = \frac{8}{3\sqrt{2}} \)
問題6(2)まではこのページにはありません。 これは直接代入しても答えは出ます。 ひたすら計算すれば答えは出ますよね。 中学生にはルート計算することを求めているのかもしれませんが、 ちょっとした方針を持っていれば、 また、-と-の数字をかけると+になることも中学校数学で習いますが、ルートの計算でも同様ですので次のように計算できます。 √4×√4=(-2)×(-2)=4 つまり、√4の答えには2と-2の2つが存在するということです。 平方根(ルート)の計算方法と/1/7 2年一次関数総合問題Lv3 5(2) 点Pはlとx軸の交点(誤)→点Bはlとx軸の交点(正) 3年方程式文章題(割合2)3(1)解答 2番目の式 yの係数 97 100 (誤)→ 93 100 (正) 7 3年2乗に比例する関数総合問題4 5問題 点A, P, Qを頂点とする(誤)→点D, P, Qを頂点とする(正)
平方根 (ルートの四則計算) ルートの計算の加減乗除、つまり四則混合の問題です。 それぞれの基礎ができていれば自信をもって取り組んでください。 自信がない人はまずは前にもどって加減乗除それぞれの計算方法を復習しましょう。 ルートは常に簡単にできないかどうかを考えてくだ 平方根の計算についてもこれは同じで、ルートの中身が違った場合、平方根の値が変わってきてしまうため、そのまま足したり引いたりすることができないのです。 では、次に少し応用の問題を解いてみましょう。 √12√75√48 この計算をしてみてください。 logの問題でルートが出てきたときはどうやって計算しますか?例えば、a=log10 2 , b=log10 3 の時 log10 √12 だったらどうなりますか?これでいいかな?




二重根号とは 外し方は 例題を用いて詳しく解説 高校生向け受験応援メディア 受験のミカタ




中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
平方根の大小を比べる問題です。 テストにもよく出題されますので、確実に出来るようにしておきましょう。 平方根の大小・基本 a,bが正の数で a < b ならば < ルートがついたものどうしは、ルートの中の数字をくら平方根整数 (入試問題) → 携帯版は別頁 == 根号計算の入試問題 == ※以下に引用する高校入試問題で,元の問題は記述式の問題ですが,web画面上で入力問題にすると操作性が悪いので,選択問題に書き換えています. 問題1 (画面上で解答するには,選択肢の中から正しいものを1つクリック) (1) を計算せよ。 (長崎県17年入試問題)この式はどうかな。 (x+a) 2 と同じカタチ をしているよね。 (x+a) 2 =x 2 +2ax+a 2 の公式が使えるから、(√3+2) 2 =(√3) 2 +2×√3×2+2 2 と展開できるね。 ②の答え (√6+√3) 2 も (x+a) 2 と同じカタチ をしているよね。 (√6+√3) 2 =(√6) 2 +2×√6×√3+(√3) 2 と展開できるね。




中学数学 平方根 のコツ 有理化 加減乗除 展開




塾ノート 中3 数学 平方根 中学生 数学のノート Clear
問次の式を計算せよ。101~ (2) √2+√32-√72=254~ (3) (2√5+3√6)-(√96-√45)=519~ (4) (2√3-√6) (√3+3√6)=9問題1 次の式を計算してください.負の数のルートが登場するときは,虚数単位 i を使って表してください. (右の選択肢から選んでください) 3ルートの割り算も文字式に変換して計算! さて、次式のような計算問題はどう解けば良いでしょう。 ・・・① ここで問題なのが、『どれとどれを割ることができるか』を理解できているか否かです。 覚えましょう!
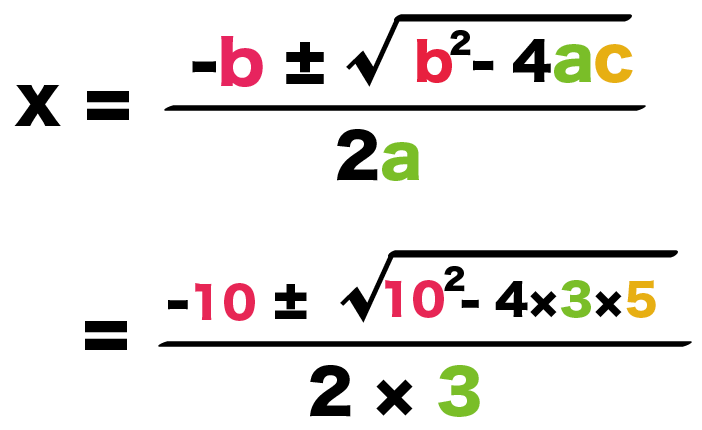



簡単計算 解の公式の問題のやり方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 ルート分数の掛け算の2つの練習問題 Qikeru 学びを楽しくわかりやすく
問題 次のルート(平方根)の中の値を簡単にする問題を解きましょう。 ルートの中の値が簡単にできればルートの計算はやりやすくなるので簡単にする方法を覚えてください。 問1. 平方根とは、どういう意味ですか? 問2.詳細 問題例の大きさは、都市の数で表される。この問題は、計算複雑性理論においてnp困難と呼ばれる問題のクラスに属する。 すなわち、問題例の大きさに関する決定性の多項式時間アルゴリズムが見つかりそうにない、計算量的に困難な問題である。 。なお、この問題の特殊ケースとして平方根 例題 平方根1 平方根2 循環小数1 循環小数2 平方根の大小1 平方根の大小2 平方根の積と商 ルートの変形1 ルートの変形2 有理化 ルートの乗法除法1 ルートの加法減法1 ルートの加法減法2 (変形) ルートの加法減法3 (分数) 平方根のおよその値 平方根の四則計算 平方根のいろいろな計算 (分配法則) 平方根_式の値 平方根の性質 (自然数になる) 平方根の性質 (自然数に



1




質問の回答 平方根を含んだ計算問題の解説 脱 会社員生活
指数法則とは? 公式・証明や、分数・ルートを含む計算問題 21年2月19日 この記事では、「指数法則」の公式や意味をできるだけわかりやすく解説していきます。 指数法則の証明や、分数やルートを含む計算問題の解き方も紹介していきますので、この ルートの掛け算の計算 がある。 ルートの掛け算の基本は、 ルートの中身を掛け算するだけ だったよね?? そんなむずくなさそう。 だけどね、実際の計算問題だとそうはいかない。 そんなに世間は甘くないんだ。ルートの計算の解説 ルート同士で四則演算をおこなう場合、足し算・引き算と掛け算・割り算では計算方法が異なります。 ルートの足し算・引き算 ルートの足し算・引き算をおこなう場合は、ルート内の数は同じで



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係




中3数学 ルートの計算とカッコ カッコの公式 練習編 映像授業のtry It トライイット
平方根 例題 平方根1 平方根2 循環小数1 循環小数2 平方根の大小1 平方根の大小2 平方根の積と商 ルートの変形1 ルートの変形2 有理化 ルートの乗法除法1 ルートの加法減法1 ルートの加法減法2 (変形) ルートの加法減法3 (分数) 平方根のおよその値 平方根の四則計算 平方根のいろいろな計算 (分配法則) 平方根_式の値 平方根の性質 (自然数になる) 平方根の性質 (自然数にルートの中はできるだけ簡単にする。 例 8 = 2 2 3 2 2 6 38 3 = 3 × 2 2 × 2 2 6 32 2 × 3 3 × 3 = 6 2 2 6 32 6 3 = 6 2 98 × 50 = 7 2 ×5 2 = 35 4 = 70 12 60 ÷3 10 = 12 3 60 10 = 4 6 2 3 6 ÷ 4 3 2 × 7 2 5 ↓割り算を逆数の掛け算にする = 2 3 6 × 3 4 2 × 7 2 5 ↓ルートの外は外どうし、中は中どうし計算 = 2×3×7 3×4×2 × 6 × 5 2 ↓約分 = 7 4 15 2 3 ×3 2 12 6 ↓分母の有理化



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




ルートの値を代入する問題 色んな知識を使う良い問題です 中学や高校の数学の計算問題




平方根 ルート の足し算と引き算のやり方と計算問題 中学3年生数学 Irohabook




ルートの足し算のやり方 簡単すぎる例題問題を解いてみよう 中学や高校の数学の計算問題



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス
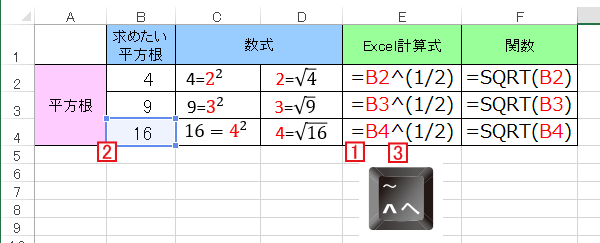



愛されし者 ルート 計算 足し算



平方根の筆算のしかた




平方根を簡単にする 3つの方法 Wikihow




平方根 とは何か 計算方法 覚え方 どう役に立つのかを解説 アタリマエ




中学3年生 数学 平方根の加法 減法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




数学問題集の部屋 平方根の計算 入試問題1の解答
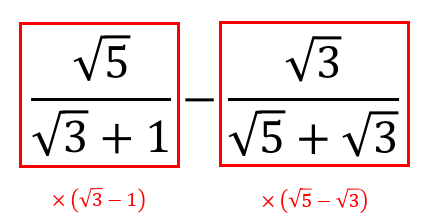



ルートの分数計算 問題解説で完全マスターだ 数スタ
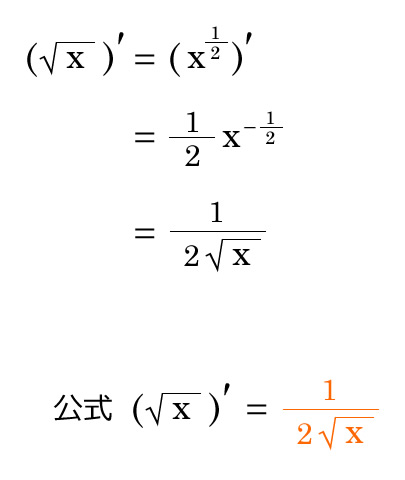



平方根の微分 優技録




簡単な計算問題です 代数 ルートの計算です Clear




ルート の 問題 ニスヌーピー 壁紙




平方根 ドリるーむ



平方根の計算 平方根のチョー簡単な問題をまとめたよ 三重の個人契約家庭教師



Q Tbn And9gcqrowgvqn H0mpsul5gslm5oso Kohgdb3kvug Q8m84kyw0il Usqp Cau




無料 中3数学 発展 応用問題 問題プリント 314 平方根6 いろいろな計算1



最高のコレクション ルート 展開 計算機 ハイキュー ネタバレ




整数をルートにする方法 5秒で計算できる簡単な問題だ 中学や高校の数学の計算問題
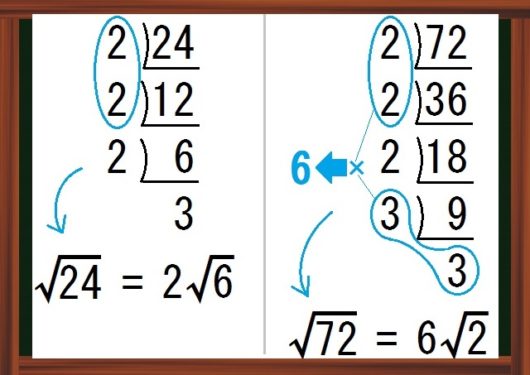



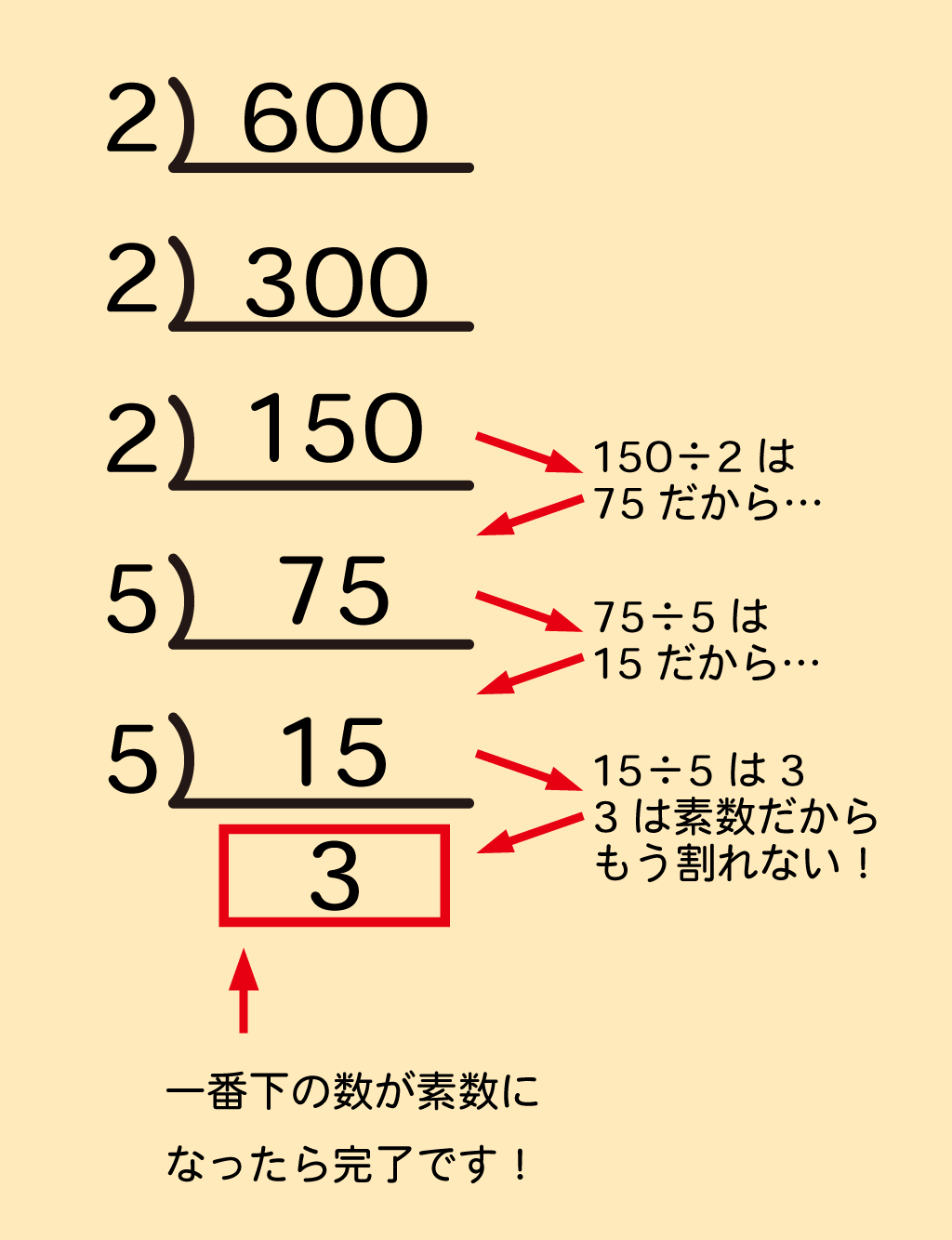
中学数学 平方根 のコツ 素因数分解 ルートを簡単にする計算




中3 数学 無料学習プリント教材



数学 中3 18 ルートのかけ算 わり算 Youtube




数学 中3 21 ルートの計算のまとめ Youtube



平方根の掛け算は 1分でわかる意味 計算のやり方 公式 分数の掛け算



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス



3




平方根 ルート の重要な計算方法まとめ 数学fun




平方根 ルートとは 平方根の求め方を解説 分数や小数の場合はどうやる 数スタ




中3 数学 無料学習プリント教材




中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中3数学の基本問題プリント 問題と解答




中学生向け 無理数の整数部分と小数部分 京橋数学塾a4u
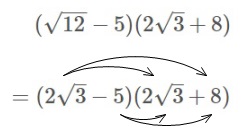



展開公式を利用するルートのついた無理数の計算問題とポイント



1




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




数と式 平方根について 日々是鍛錬 ひびこれたんれん



数学のルートの問題がわかりません 青で囲んだ部分はどうやった計 Yahoo 知恵袋




ルートの四則演算 計算する順番に注意しよう 中学や高校の数学の計算問題




中3数学 ルートの計算とカッコ カッコの公式 練習編 映像授業のtry It トライイット
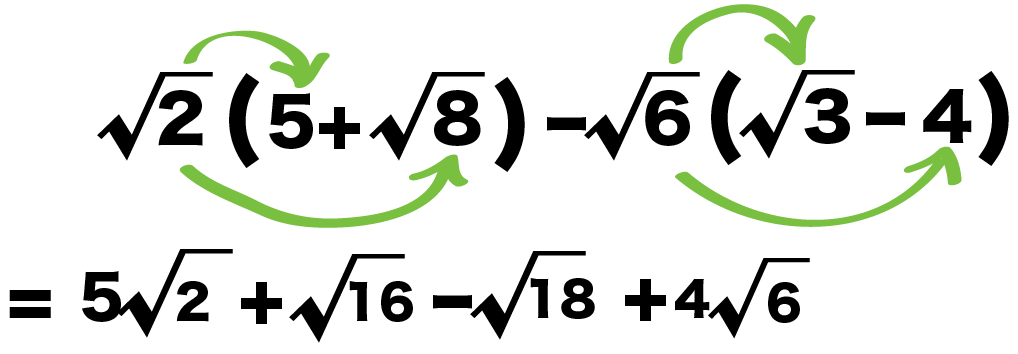



平方根の式を分配法則で計算する4つのステップ Qikeru 学びを楽しくわかりやすく




中学3年生 数学 平方根の乗法 除法 問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中学数学の二次方程式の問題です 画像の問題を解の公式を使い答えなさい Yahoo 知恵袋




世界一わかりやすい数学問題集中3 2章 平方根
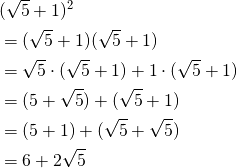



ルート 根号 の計算方法をマスターしよう スタディクラブ情報局




中3数学 ルートの計算とカッコ カッコの公式 練習編 映像授業のtry It トライイット




数 定積分 21年度京都大学文系数学2番 基本ですが どの計算ルートがミスしやすいか自分の計算力を検証するにはいいかも 学習村の 国公立へ行こう




平方根の応用 無料で使える中学学習プリント




平方根はこれで完璧 平方根の定義からルートの計算 近似値の問題の解き方まで
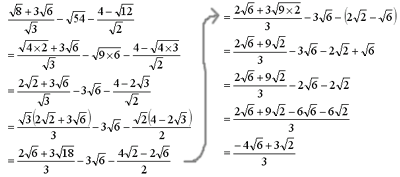



中学の数学 ルートの計算方法って Sakura Scope
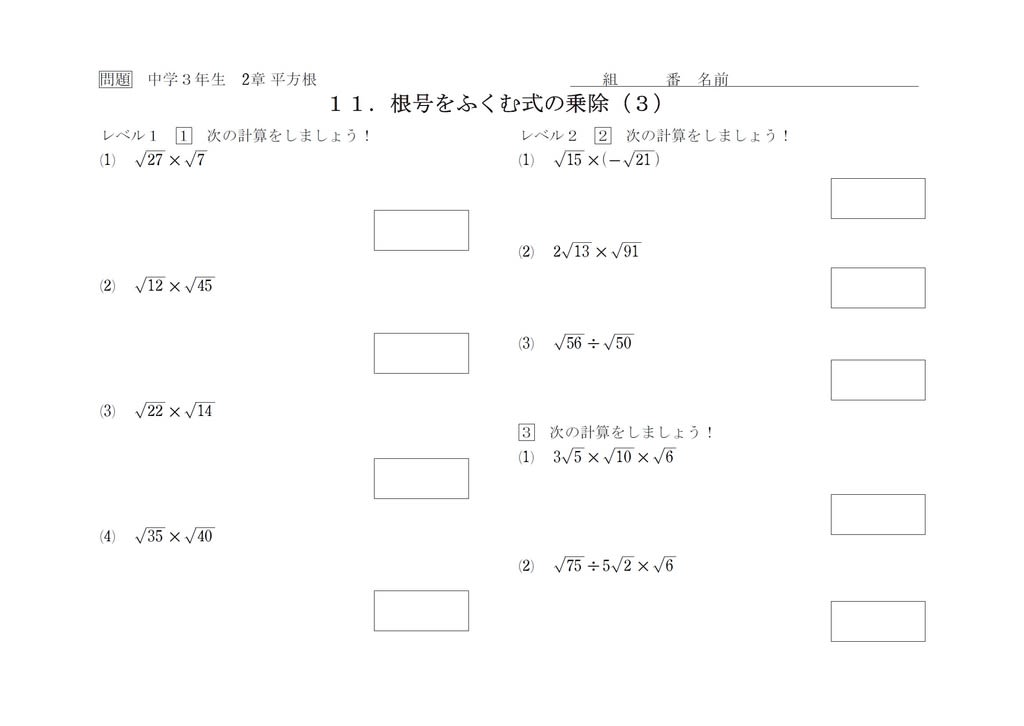



中3 平方根11 乗除3 中学数学の勉強に




平方根 べき乗 Nのm乗 平方根 ルート 立方根を利用 Excel エ Unxqaz




の中を出来るだけ簡単な数にして表す問題です 分数はどうするのですか Clear




ルートの計算
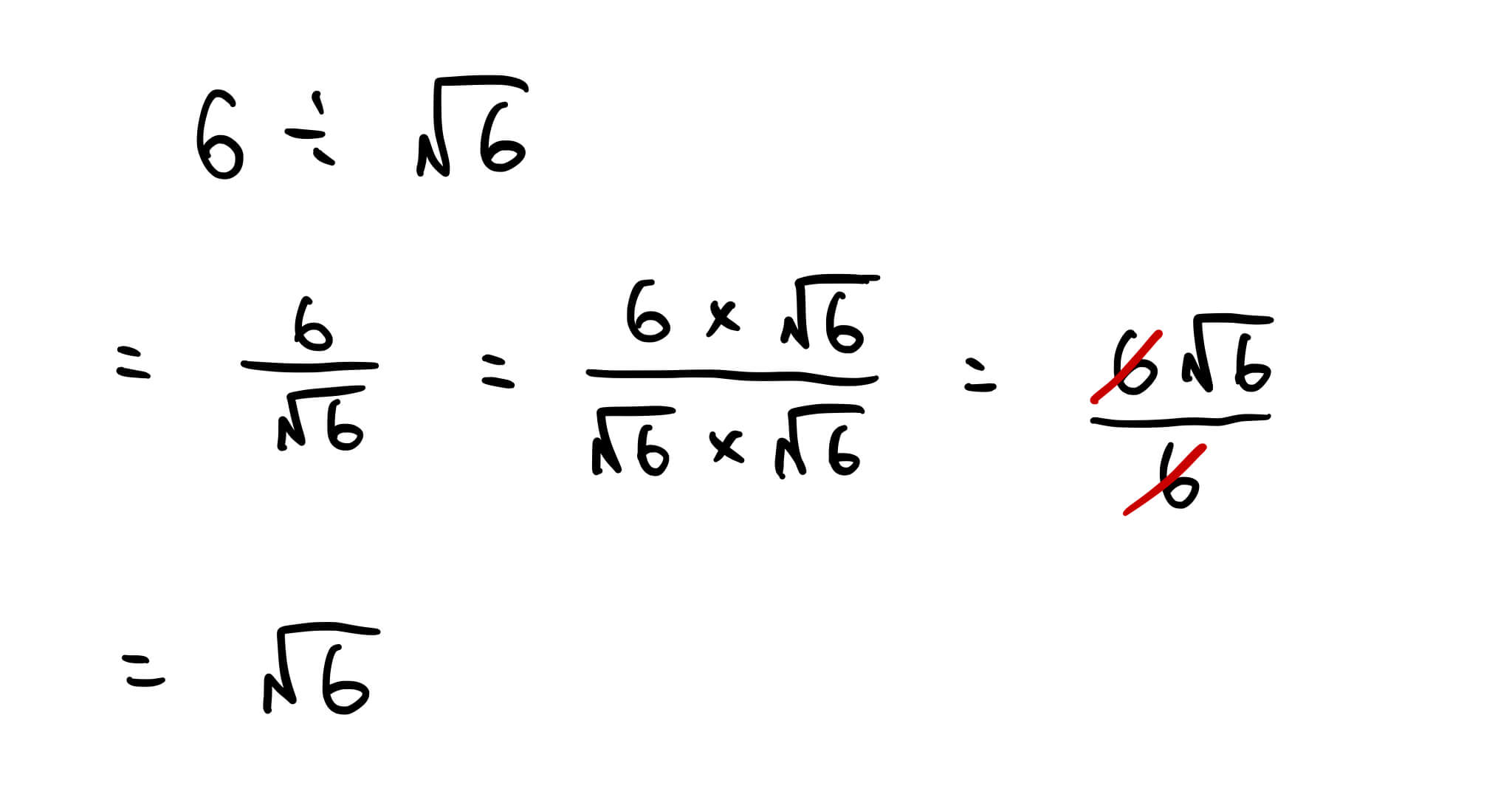



有理化問題をあえて有理化せずに解く 個太郎塾ふじみ野教室




中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




中3 数学 無料学習プリント教材



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係
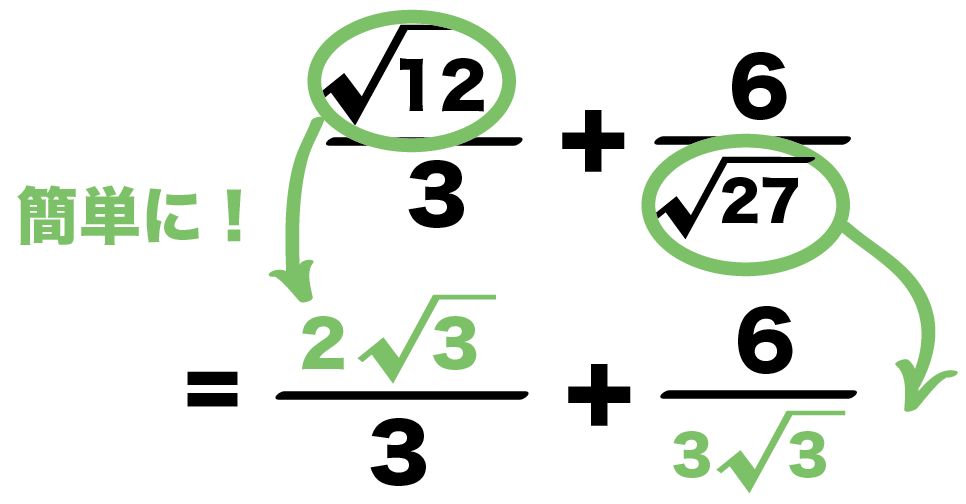



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
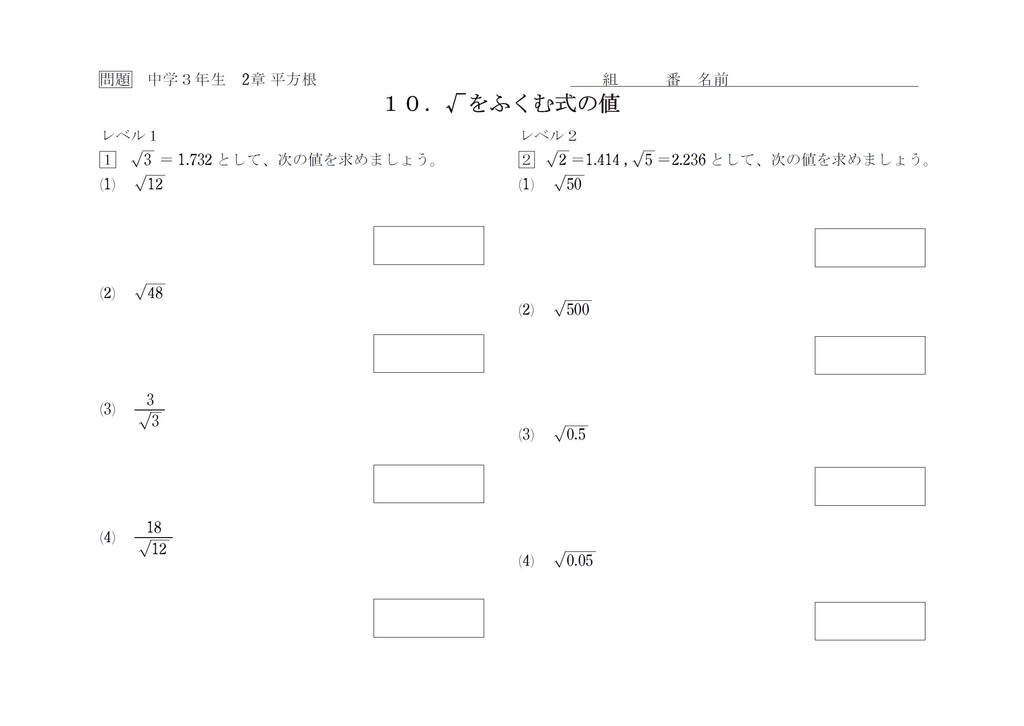



中3 平方根10 近似値 中学数学の勉強に




平方根の足し算と引き算 ルート計算のやり方や分数の求め方 リョースケ大学
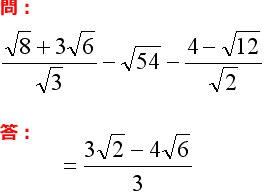



中学の数学 ルートの計算方法って Sakura Scope
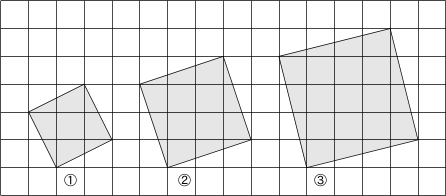



平方根応用 図形




中3数学 平方根 乗法公式を利用する計算問題 Youtube



Studydoctor根号 ルートと式の値 中3数学 Studydoctor
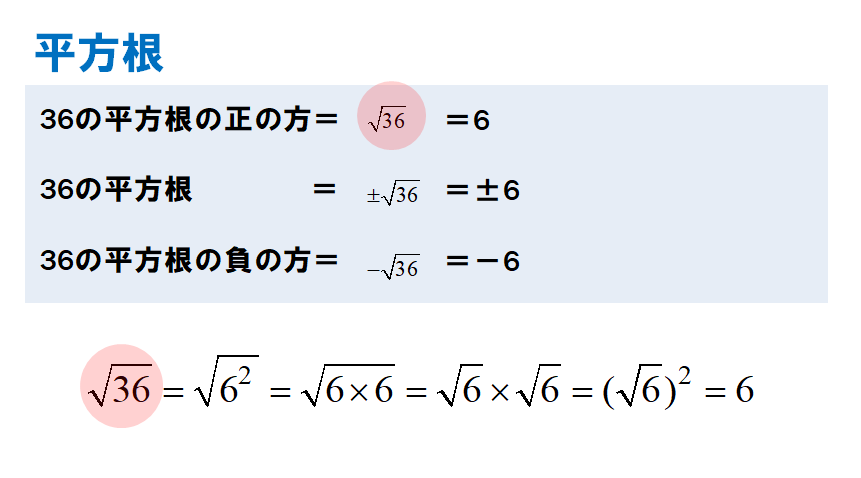



中3数学 平方根の性質の定期テスト対策問題 Examee




指数法則を使う問題の計算練習 高校数学の知識庫




平方根 ルート の足し算 引き算の仕方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




かっこのルートを二乗する問題 を外すだけなので簡単 中学や高校の数学の計算問題




ルートの割り算の問題 やり方は を合体して中で割るだけだ 中学や高校の数学の計算問題
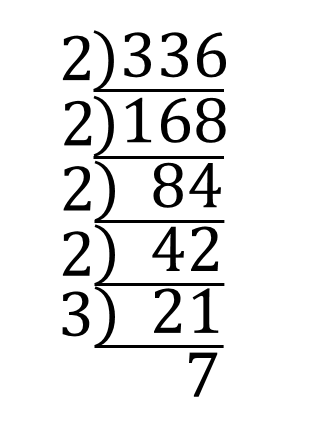



平方根 ルートの計算方法まとめ 問題を使って徹底解説 数スタ




数学 平方根 全27頁pdf版 建築学生が学ぶ構造力学 Booth




平方根を求める 問題 Youtube




平方根の計算 やり方は をつけてルートをつけよう 中学や高校の数学の計算問題




中学数学 平方根のひみつ 都立高校入試で成功する方法




数学問題集の部屋 平方根の計算 2の問題解答
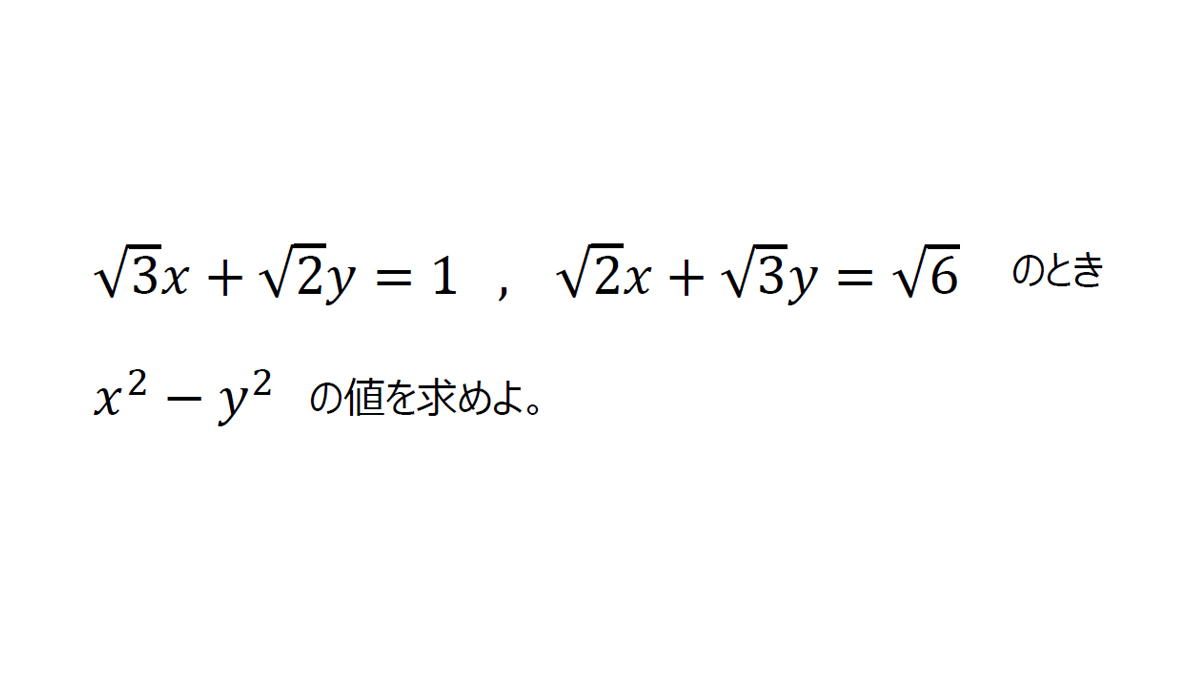



みんなの算数オンライン در توییتر 高校入試第22弾 東大寺学園高等学校19 平方根 ルート の計算問題です 式あれこれ変形させる力が数学では重要になってきますね このあたりが算数と数学の違いの1つでしょうか 解説はこちら T Co Yglxv25o1e 中学数学




中学数学3年 いろいろな平方根の計算 平方根と式の値 受験の月




ルートの応用問題 を変形して 計算できるようにする 中学や高校の数学の計算問題




Youtube Lesson 中3 平方根 第6回 根号を含む式の計算 和と差 桂坂数学教室
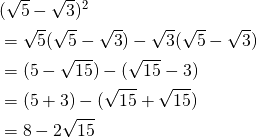



ルート 根号 の計算方法をマスターしよう スタディクラブ情報局




ルート計算 展開公式をつかう3つの平方根問題の解き方 Qikeru 学びを楽しくわかりやすく
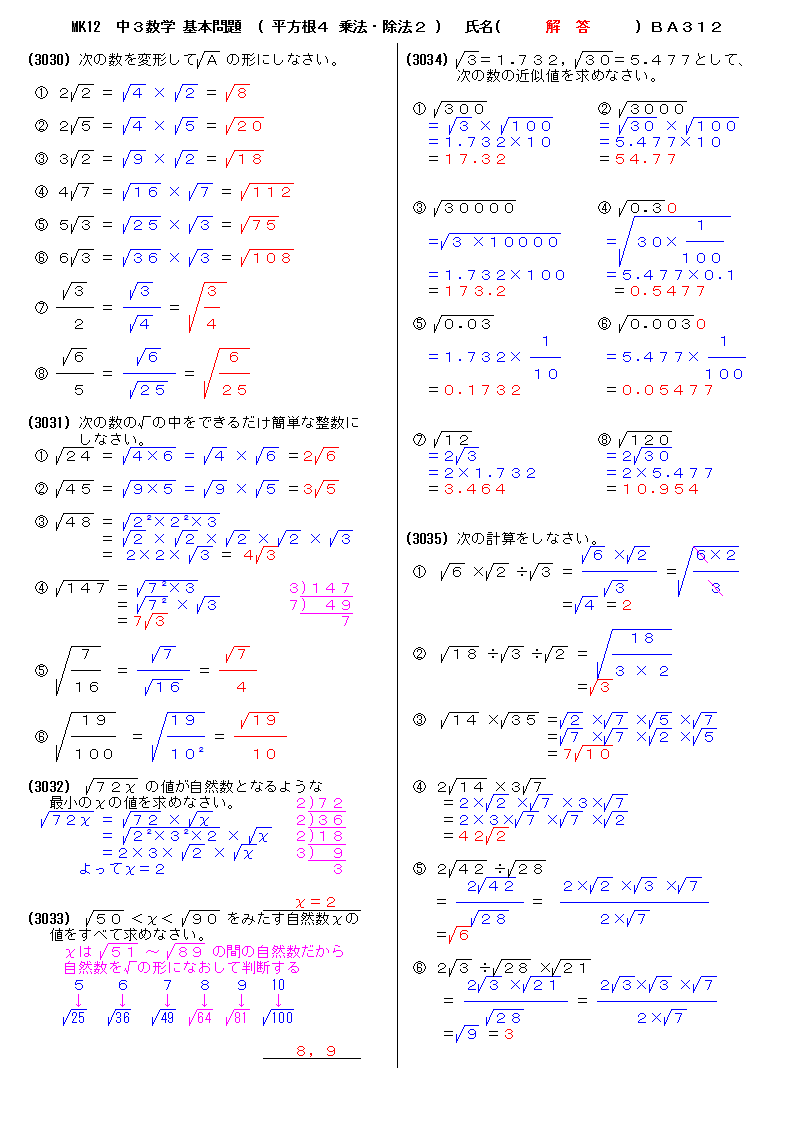



心に強く訴える中3 数学 ルート 問題 最高のカラーリングのアイデア




高校数学 因数分解 解の公式を使ってルートが登場する因数分解を解けるようになろう 数学の面白いこと 役に立つことをまとめたサイト



中学3年生向け 平方根はこうやって解く 平方根を基本から徹底解説 学習内容解説ブログ




平方根 1 基本のルール バカでもわかる 中学数学




世界一わかりやすい数学問題集中3 2章 平方根




平方根とは 東大生が平方根の計算方法や覚え方を伝授 高校生向け受験応援メディア 受験のミカタ




中3数学 練習プリントが無料でダウンロード 印刷できます ドリるーむ



Studydoctor ルートのかけ算と割り算 中3数学 Studydoctor




対数 Log の計算問題 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
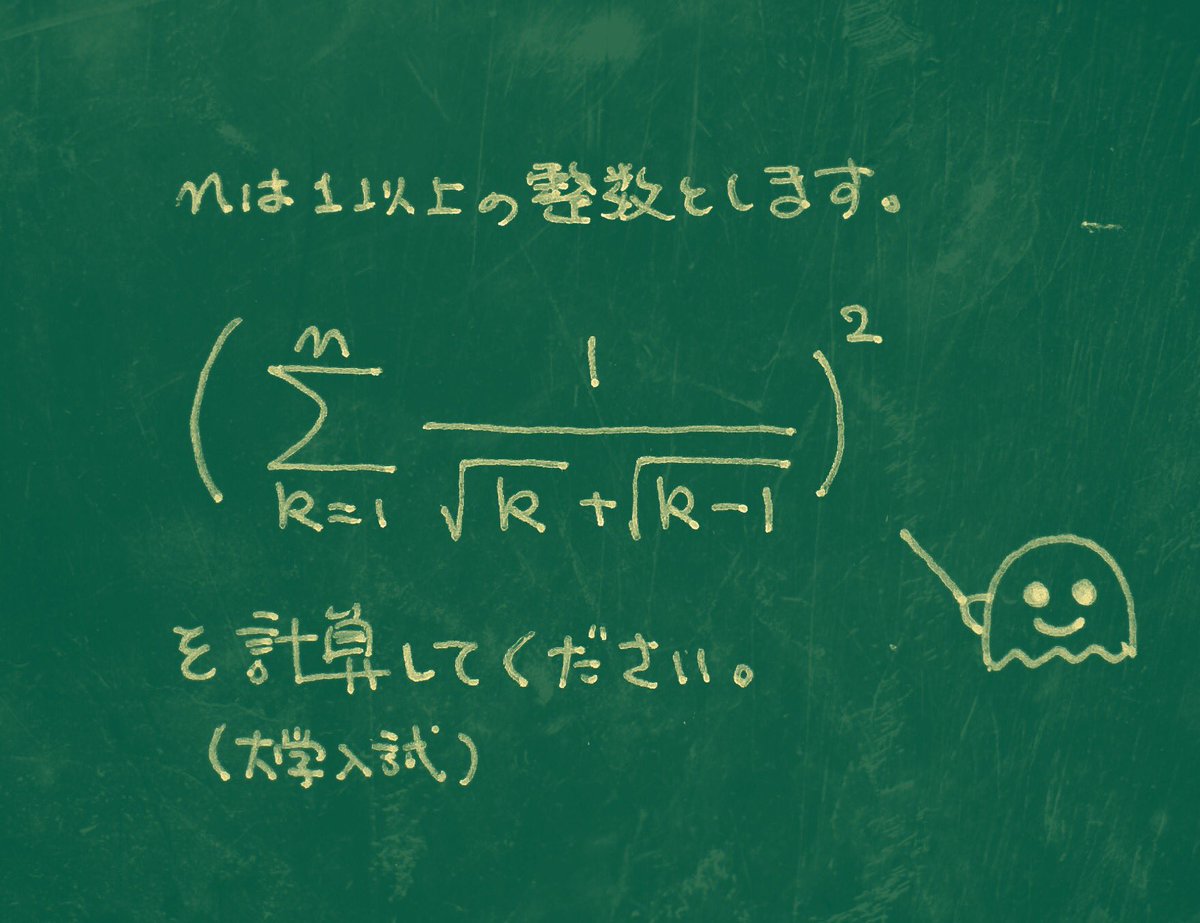



ルートとシグマが出てくる計算 結城浩の数学ノート



数学i Aチェック リピート 第1章 2実数 6 式の値 ルートをはずす Pukiwiki



0 件のコメント:
コメントを投稿